Evaluate the following Integrals:
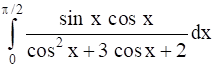
Let ![]()
In the denominator, we can write
cos2x + 3 cos x + 2 = (cos x + 1)(cos x + 2)
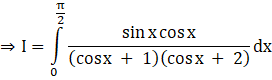
Put cos x = t
⇒ –sin(x)dx = dt (Differentiating both sides)
⇒ sin(x)dx = –dt
When x = 0, t = cos 0 = 1
![]()
So, the new limits are 1 and 0.
Substituting this in the original integral,
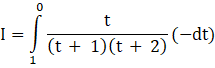
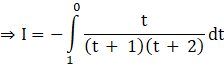
We can write,
![]()
![]()
Using this, we have
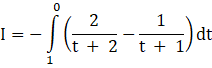

Recall ![]()
![]()
⇒ I = – [2(ln|0+2| – ln|1+2|) – (ln|0+1| – ln|1+1|)]
⇒ I = – [2(ln 2 – ln 3) – (ln 1 – ln 2)]
⇒ I = – (2 ln 2 – 2 ln 3 – 0 + ln 2)
⇒ I = – (3 ln 2 – 2 ln 3)
⇒ I = 2 ln 3 – 3 ln 2
⇒ I = ln 9 – ln 8 = ln ![]()
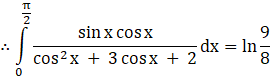
56