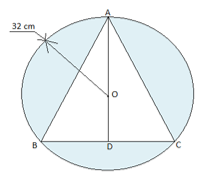
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).
Radius (r) of circle = 32 cm
AD is the median of triangle ABC
AO = 
AD = 32
AD = 48 cm
In triangle ABD,
AB2 = AD2 + BD2
AB2 = (48)2 + (AB/2)2
= (48)2
AB = 
= 
= 32√3 cm
Area of equilateral triangle, ABC = 
* (32√3)2
= 
* 32 * 32 * 3
= 96 * 8 * √3
= 768√3 cm2
Area of design = Area of circle - Area of ΔABC
= (
- 768√3) cm2
6