Show that Ax 2 + By 2 =1 is a solution of the differential equation

Question

Philoid · Accepted Answer

The differential equation is and the function to be proven as the solution is Ax² + By² =1, now we need to find the value of and .

Putting the values in the equation,

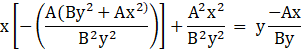
As, L.H.S = R.H.S. the equation is satisfied, so hence this function is the solution of the differential equation.

Show that Ax2 + By2 =1 is a solution of the differential equation