Solve the following differential equations:

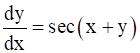
Given Differential Equation is:

⇒ ……(1)

Let us assume z = x + y

Differentiating w.r.t x on both sides we get,

⇒

⇒

⇒ ……(2)

Substituting (2) in (1) we get,

⇒

⇒

Bringing like variables on same side(i.e, variable seperable technique) we get,

⇒

We know that

⇒

⇒

We know that cos2z = cos²z – sin²z = 2cos²z – 1

⇒

⇒

⇒

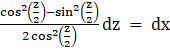
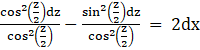
We know that 1 + tan²x = sec²x

⇒

⇒

Integrating on both sides we get,

⇒

We know that:

(1) ∫sec²xdx = tanx + C

(2) ∫adx = ax + C

⇒

Since z = x + y, we substitute this,

⇒

⇒

⇒

∴ the solution for the given differential equation is .