Solve the following differential equations :

(i) If a differential equation is ,

then y(I.F) = ∫Q.(I.F)dx + c, where I.F = e^∫Pdx

(ii) ∫dx = x + c

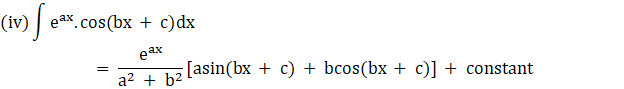
Given:-

This is a linear differential equation, comparing it with

P = 1, Q = cosx

I.F = e^∫Pdx

= e^∫dx

= e^x

Solution of the equation is given by

y(I.F) = ∫Q.(I.F)dx + c₁

⇒ y e^x = ∫cosx. e^x dx + c₁

let I = ∫ e^x cosxdx

= cosx∫ e^xdx ∫(sinx∫e^xdx)dx + c₂

using integrating by part

I = e^x cosx + ∫sinxe^xdx + c

= e^x cosx [sinx∫e^xdx∫(cosx∫e^xdx)dx] + c₂

⇒ I = e^x cosx + sinxe^x–I + C₂

⇒ 2I = (cosx + sinx)e^x + C₂

putting I