If are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3 AB and that a point D in BA produced such that BD = 2 BA.

Question

Philoid · Accepted Answer

Given the position vectors of points A and B are and.

Let the position vectors of points C and D be and.

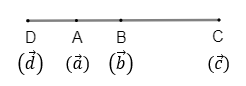
We have AC = 3AB.

From the above figure, observe AB = AC – BC

⇒ AC = 3 (AC – BC)

⇒ AC = 3AC – 3BC

⇒ 2AC = 3BC

∴ AC : BC = 3 : 2

So, C divides AB externally in the ratio 3:2.

Recall the position vector of point P which divides AB, the line joining points A and B with position vectors and respectively, externally in the ratio m : n is

Here, m = 3 and n = 2

So, the position vector of C is

We also have BD = 2BA.

From the figure, observe BA = BD – AD

⇒ BD = 2 (BD – AD)

⇒ BD = 2BD – 2AD

⇒ BD = 2AD

∴ BD : AD = 2 : 1

So, D divides BA externally in the ratio 2:1.

We now use the same formula as earlier to find the position vector of D.

Here, m = 2 and n = 1

Thus, the position vector of point C is and the position vector of point D is .