Show that the four points A, B, C, D with position vectors respectively such that are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.

Question

Philoid · Accepted Answer

Given the position vectors of points A, B, C and D are,, and respectively.

We have

Rearranging the terms in the above equation,

Observe that the sum of coefficients on the LHS of this equation (3 + 5 = 8) is equal to that on the RHS (2 + 6 = 8).

We now divide the equation with 8 on both sides.

Now, consider the LHS of this equation.

Let , the position vector of some point X.

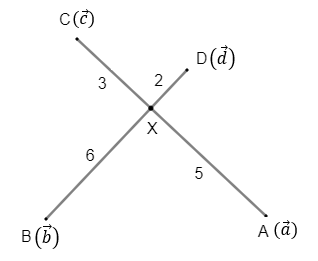
Recall the position vector of point P which divides AB, the line joining points A and B with position vectors and respectively, internally in the ratio m : n is

Here, m = 3 and n = 5

So, X divides CA internally in the ratio 3:5.

Similarly, considering the RHS of this equation, we have the same point X dividing DB in the ratio 2:6.

So, the point X lies on both the line segments AC and BD making it the point of intersection of AC and BD.

As AC and BD are two straight lines having a common point, we have all the points A, B, C and D lying in the same plane.

Thus, the points A, B, C and D are coplanar and in addition, the position vector of the point of intersection of line segments AC and BD is or.