The vertices A, B, C of triangle ABC have respectively position vectors ![]() with respect to a given origin O. Show that the point D where the bisector of ∠A meets BC has position vector
with respect to a given origin O. Show that the point D where the bisector of ∠A meets BC has position vector  where
where ![]() and
and ![]()
Given the position vectors of vertices A, B and C of ΔABC are ![]() and
and ![]() respectively.
respectively.
D is point on BC with position vector![]() such that AD is the bisector of ∠A. I is the incenter of ΔABC.
such that AD is the bisector of ∠A. I is the incenter of ΔABC.
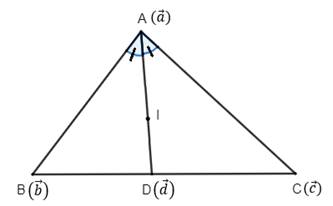
Observe from the figure that D divides BC in the ratio BD:DC.
Using the angular bisector theorem, we know that the angle bisector of an angle in a triangle bisects the opposite side in the ratio equal to the ratio of the other two sides.
![]()
But, ![]() and
and![]() .
.
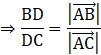
Recall the vector ![]() is given by
is given by
![]()
![]()
Similarly, ![]()
So, we have ![]() .
.
Recall the position vector of point P which divides AB, the line joining points A and B with position vectors ![]() and
and ![]() respectively, internally in the ratio m : n is
respectively, internally in the ratio m : n is
![]()
Here, we have D dividing BC internally in the ratio m:n where m = BD = ![]() and n = DC =
and n = DC = ![]()
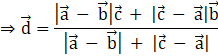
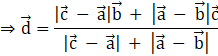
Suppose ![]() and
and![]() .
.
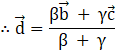
From angular bisector theorem above, we have![]() .
.
Adding 1 to both sides,
![]()
![]()
![]()
![]()
In addition, as CI is the angular bisector of ∠C in ΔACD, using the angular bisector theorem, we have
![]()
So, we get ![]()
We have ![]() and
and ![]()
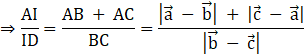
Assume ![]()
![]()
So, I divides AD in the ratio (β + γ):α.
Let the position vector of I be ![]() .
.
Using the aforementioned section formula, we can write
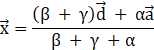
But, we already found![]() .
.
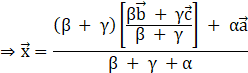
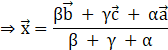
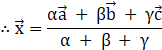
Thus, ![]() and the position vector of the incenter is
and the position vector of the incenter is ![]() , where
, where![]() ,
, ![]() and
and ![]() .
.