If O is a point in space, ABC is a triangle and D, E, F are the mid-points of the sides BC, CA and AB respectively of the triangle, prove that

Let position vectors of the vertices A, B and C of ΔABC with respect to O be , and respectively.

⇒

Let us also assume the position vectors of the midpoints D, E and F with respect to O are, and respectively.

⇒

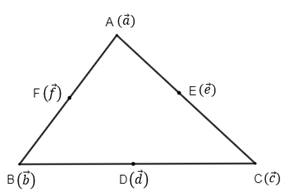
Now, D is the midpoint of side BC.

This means D divides BC in the ratio 1:1.

Recall the position vector of point P which divides AB, the line joining points A and B with position vectors and respectively, internally in the ratio m : n is

Here, m = n = 1

Similarly, for midpoint E and side CA, we get and for midpoint F and side AB, we get .

Adding these three equations, we get

Thus, .