Show that the sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.

Consider a ΔABC with D, E and F being the midpoints of sides BC, CA and AB respectively.

Let the position vectors of these vertices and midpoints be as shown in the figure.

We need to prove.

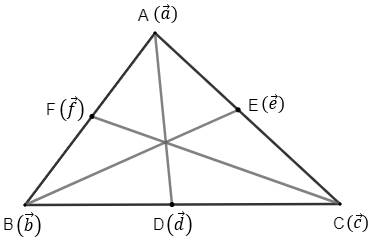
As D is the midpoint of BC, using midpoint formula, we have

Similarly, and.

Recall the vector is given by

Similarly, and

Now, consider the vector.

But, and

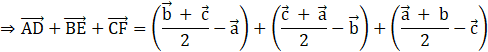
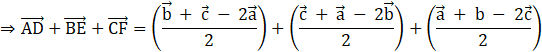
Thus, the sum of the three vectors determined by the medians of a triangle is zero.