ABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD ; BC and AD. Show that where P is any point.

Question

Philoid · Accepted Answer

Let E, F, G and H be the midpoints of sides AB, BC, CD and DA respectively of quadrilateral ABCD.

Let the position vectors of these vertices and midpoints be as shown in the figure.

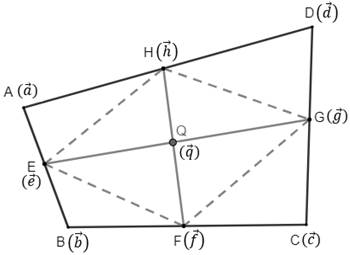
As E is the midpoint of AB, using midpoint formula, we have

Similarly, , and .

We know that the line segments joining the midpoints of opposite sides of a quadrilateral bisect each other.

⇒ Q is the midpoint of EG and HF.

Once again using midpoint formula, we get

But, we found and .

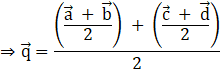
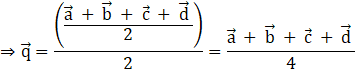
Now, consider the vector .

Let the position vector of point P be .

Recall the vector is given by

Similarly, , and .

But, we found

Observe,

Thus,