Find the area of the region between circles x² + y² = 4 and (x – 2)² + y² = 4.

The given equations are,

x² + y² = 4 ...(i)

(x – 2)² + y² = 4 ...(ii)

Equation (i) is a circle with centre O at origin and radius 2.

Equation (ii) is a circle with centre C (2,0) and radius 2.

On solving these two equations, we have

(x – 2)² + y² = x² + y²

Or x² – 4x + 4 + y² = x² + y²

Or x = 1 which gives y ± √3

Thus, the points of intersection of the given circles are A (1, √3) and A’ (1, – √3) as show in the graph below

Now the bounded area is the required area to be calculated, Hence,

Required area of the enclosed region OACA’O between circle

A = [area of the region ODCAO]

= 2 [area of the region ODAO + area of the region DCAD]

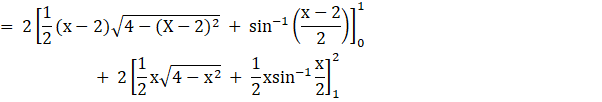
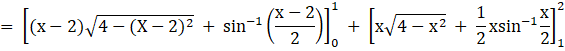
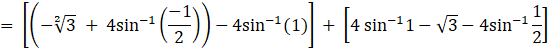
The area of the region between circles x² + y² = 4 and (x – 2)² + y² = 4 is