Draw a rough sketch of the region {(x,y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using the method of integration.
To find the area enclosed by the region{(x,y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36}
The given equations are,
y2 = 5x ...(i)
And 5x2 + 5y2 = 36 ...(ii)
![]()
Substituting the value of y2 from (i) into (ii)
5x2 + 25x = 36
5x2 + 25x – 36 = 0
x = ![]()
Equation (i) represents a parabola with vertex (0, 0) and axis as x - axis.
Equation (ii) represents a circle with centre (0, 0) and radius 6/√5 and meets axes at ![]() and
and ![]() . X ordinate of the point of intersection of circle and parabola is A where a =
. X ordinate of the point of intersection of circle and parabola is A where a = ![]() .
.
A rough sketch of curves is: -
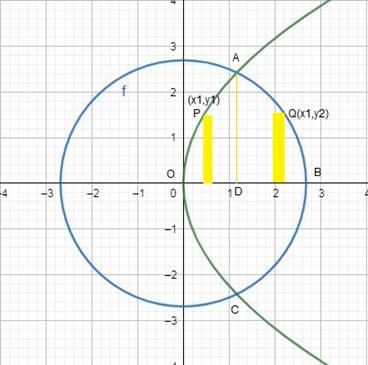
Required area = Region OCBAO
= 2 (Region OBAO)
= 2 (Region ODAO + Region DBAD)
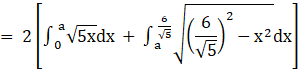
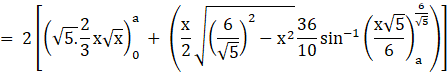
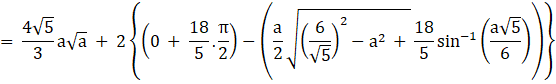
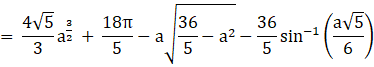
![]()
The area enclosed by the region ![]() is
is ![]() sq. Units
sq. Units