Find the area included between the parabolasy2 = 4ax and x2 = 4by.
To find area enclosed by
Y2 = 4ax
![]() ...(i)
...(i)
And X2 = 4by
![]() ...(ii)
...(ii)
On solving the equation (i) and (ii),
![]()
Or, x4 – 64ab2x = 0
Or, x(x3 – 64ab2) = 0
Or, x = 0 and x = ![]()
Then y = 0 and y = ![]()
Equation (i) represents a parabola with vertex (0,0) and axis as x–axis,
Equation (ii) represents a parabola with vertex (0,0) and axis as x - axis,
Points of intersection of parabolas are O (0,0) and ![]()
These are shown in the graph below: -
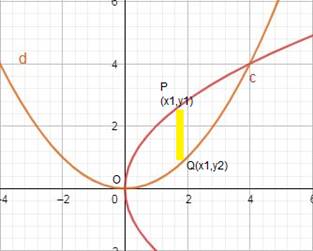
The shaded region is required area, and it is sliced into rectangles of width and length (y1 – y2)ΔX.
This approximation rectangle slides from![]() x = 0 to
x = 0 to ![]() , so
, so
Required area = Region OQCPO
![]()
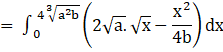

![]()
![]()
![]()
The area included between the parabolasy2 = 4ax and x2 = 4by is ![]()
16