Using the method of integration, find the area of the region bounded by the following line 3x – y – 3 = 0, 2x + y – 12 = 0, x – 2y – 1 = 0.
To find region enclosed by
3x – y – 3 = 0 ...(i)
2x + y – 12 = 0 ...(ii)
x – 2y – 1 = 0 ...(iii)
Solving (i) and (ii), we get,
5x – 15 = 0
Or x = 3
∴y = 6
The points of intersection of (i) and (ii) is B (3,6)
Solving (i) and (iii), we get,
5x = 5
Or x = 1
∴y = 0
The points of intersection of (i) and (iii) is A (1,0)
Solving (ii) and (iii), we get,
5x = 25
Or x = 5
∴y = 2
The points of intersection of (ii) and (iii) is C (5,2) .
These are shown in the graph below: -

Area of the bounded region
= ![]()
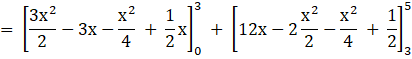
![]()
= 11 sq. units
The area of the region bounded by the following line 3x – y 3 = 0, 2x + y – 12 = 0, x – 2y – 1 = 0 is ![]()
30