In a simple circuit of resistance R, self inductance L and voltage E, the current i at any time t is given by 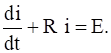If E is constant and initially no current passes through the circuit, prove that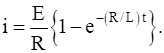

We know that in a circuit of R, L and E we have,

⇒

We can see that it is a linear differential equation of the form

Where P = and Q =

I.F = e^∫Pdt

= e^dt

=

Solution of the given equation is given by

i × I.F = ∫Q × I.F dt + c

⇒ i × = ∫ × dt + c

⇒ i × = ∫ × dt + c

⇒ i = + c ……(1)

Initially, there was no current

So, at i = 0, t = 0

Now, putting the value of c in equation (1)

i = –

i = (1 – )