Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half – life is 1590 years. What percentage will disappear in one year?
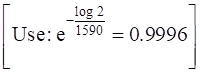
Let the quantity of radium at any time t be A.
According to question,
⇒ 
where k is a constant
⇒ 
⇒ 
Integrating both sides, we have
⇒ ∫
= – k∫dt
⇒ log|A| = – kt + c……(1)
Given, Initial quantity of radium be A0 when t = 0 sec
Putting the value in equation (1)
∴ log|A| = – kt + c
⇒ log| A0| = 0 + c
⇒ c = log| A0| ……(2)
Putting the value of c in equation (1) we have,
log|A| = – kt + log| A0|
⇒ log|A| – log| A0| = – k t [
]
⇒ log (
= – kt ……(3)
Given its half life = 1590 years,
From equation(3),we have
∴ – kt = log (
⇒ – k×1590 = log (
⇒ – k×1590 = 
⇒ – k×1590 = – log 2
⇒ k = 
∴ The equation becomes
log (
= – 
t
log (
= – 0.9996 t
Percentage Disappeared = (1 – 0.9996) × 100 = 0.04 %