A curve is such that the length of the perpendicular from the origin on the tangent at any point P of the curve is equal to the abscissa of P. Prove that the differential equation of the curve is and hence find the curve.

⇒

It is a homogenous equation,

Putting y = kx

So,

Putting the value of k

Differentiating with respect to x,

⇒

Let (h,k) be the point where tangent passes through origin and the length is equal to h. So, equation of tangent at (h,k) is

⇒

⇒ 2ky – 2k² = cx – ch – 2hx + 2h²

⇒ x(c – 2h) – 2ky + 2k² –hc + 2h² = 0

⇒ x(c – 2h) – 2ky + 2(k² –2h) – hc = 0

⇒ x(c – 2h) – 2ky + 2(ch) – hc = 0 ( h² + k² = ch as (h,k) on th curve)

⇒ x(c – 2h) – 2ky + hc = 0

Now, Length of perpendicular as tangent from origin is

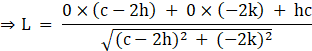
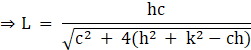
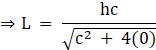
Hence, x² + y² = cx is the required curve.