Find the angle between the lines whose direction cosines are given by the equations:
2l+2m–n=0 and mn+ln+lm=0
Given relations are:
⇒ mn+ln+lm=0 ……(1)
⇒ 2l+2m–n=0
⇒ n=2l+2m ……(2)
Substituting (2) in (1) we get,
⇒ m(2l+2m)+l(2l+2m)+lm=0
⇒ 2lm+2m2+2l2+2lm+lm=0
⇒ 2m2+5lm+2l2=0
⇒ 2m2+4lm+lm+2l2=0
⇒ 2m(m+2l)+l(m+2l)=0
⇒ (2m+l)(m+2l)=0
⇒ 2m+l=0 or m+2l=0
⇒ 2m=–l or 2l=–m ……(3)
Substituting the values of (3) in (2), we get
For the 1st line:
⇒ n=2l–l
⇒ n=l
The Direction Ratios for the first line is ![]()
For the 2nd line:
⇒ n=–m+2m
⇒ n=m
The Direction Ratios for the second line is ![]()
We know that the angle between the lines with direction ratios proportional to (a1,b1,c1) and (a2,b2,c2) is given by:
⇒ 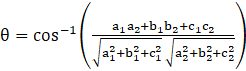
Using the above formula we calculate the angle between the lines.
Let ![]() be the angle between the two lines given in the problem.
be the angle between the two lines given in the problem.
⇒ 
⇒ 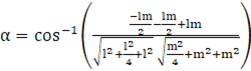
⇒ 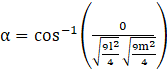
⇒ ![]()
∴ the angle between two lines is ![]() .
.