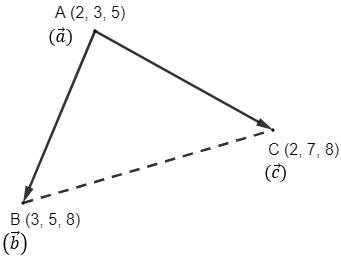
Using vectors, find the area of the triangle with vertices A(2, 3, 5), B(3, 5, 8) and C(2, 7, 8).

Given three points A(2, 3, 5), B(3, 5, 8) and C(2, 7, 8) forming a triangle.

Let position vectors of the vertices A, B and C of ΔABC be, and respectively.

We know position vector of a point (x, y, z) is given by, where, and are unit vectors along X, Y and Z directions.

Similarly, we have and

To find area of ΔABC, we need to find at least two sides of the triangle. So, we will find vectors and.

Recall the vector is given by

Similarly, the vector is given by

Recall the area of the triangle whose adjacent sides are given by the two vectors and is where

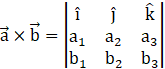
Here, we have (a₁, a₂, a₃) = (1, 2, 3) and (b₁, b₂, b₃) = (0, 4, 3)

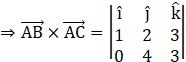
Recall the magnitude of the vector is

Now, we find.

Thus, area of the triangle is square units.