The two adjacent sides of a parallelogram are and Find the unit vector parallel to one of its diagonals. Also, find its area.

Let ABCD be a parallelogram with sides AB and AC given.

We have and

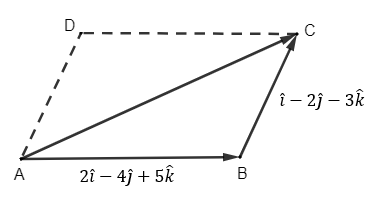
We need to find unit vector parallel to diagonal.

From the triangle law of vector addition, we have

Let the unit vector in the direction of be.

We know unit vector in the direction of a vector is given by .

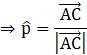
Recall the magnitude of the vector is

Now, we find.

So, we have

Thus, the required unit vector that is parallel to diaonal is.

Now, we have to find the area of parallelogram ABCD.

Recall the area of the parallelogram whose adjacent sides are given by the two vectors and is where

Here, we have (a₁, a₂, a₃) = (2, –4, 5) and (b₁, b₂, b₃) = (1, –2, –3)

Recall the magnitude of the vector is

Now, we find.

Thus, area of the parallelogram is square units.