Find all vectors of magnitude that are perpendicular to the plane of and

Given two vectors and

We need to find vectors of magnitude perpendicular to and.

Recall a vector that is perpendicular to two vectors and is

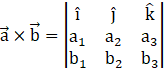
Here, we have (a₁, a₂, a₃) = (1, 2, 1) and (b₁, b₂, b₃) = (–1, 3, 4)

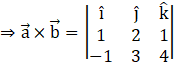
Let the unit vector in the direction of be.

We know unit vector in the direction of a vector is given by .

Recall the magnitude of the vector is

Now, we find.

So, we have

So, a vector of magnitude in the direction of is

Observe that is also a unit vector perpendicular to the same plane. This vector is along the direction opposite to the direction of vector.

Thus, the vectors of magnitude that are perpendicular to plane of both and are.