The two adjacent sides of a parallelogram are and . Find the two unit vectors parallel to its diagonals. Using the diagonal vectors, find the area of the parallelogram.

We need to find a unit vector parallel to

Now from the Parallel law of vector Addition, we know that,

Therefore,

Now we need to find the unit vector parallel to

Any unit vector is given by,

Therefore,

Now, we need to find Area of parallelogram. From the figure above it can be easily found by the cross product of adjacent sides.

Therefore, Area of Parallelogram =

If and

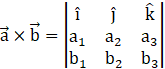
Here, we have,

(a₁, a₂, a₃) = (2, -4, -5) and (b₁, b₂, b₃) = (2, 3, 3)

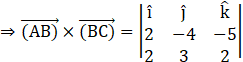
Area of Parallelogram = 21 sq units.