Find the vector equation of the plane passing through the points (1, 1, – 1), (6, 4, – 5) and (– 4, – 2, 3).

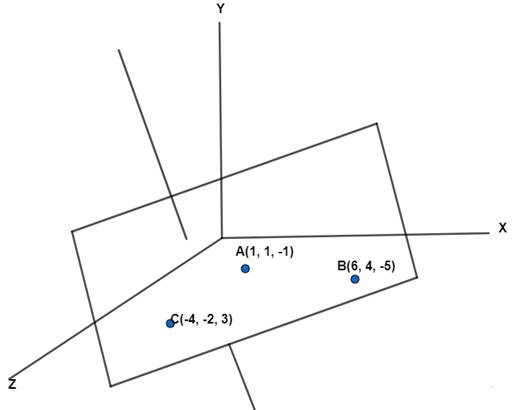
Let A(1,1, – 1), B(6,4, – 5), C(– 4, – 2 – 3).

The required plane passes through the point A(1,1, – 1), whose position vector is and is normal to the vector given by

Clearly,

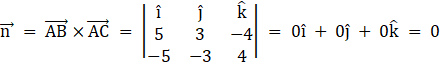
So, the given points are collinear.

Thus there will be an infinite number of planes passing through these points.

Their equations (passing through (1,1, – 1) are given by,

a(x – 1) + b(y – 1) + c(z + 1) = 0 ……(i)

Since this passes through B(6,4, – 5),

a(6 – 1) + b(4 – 1) + c(– 5 + 1) = 0

or, 5a + 3b – 4c = 0 ……(ii)

From (i) and (ii), the equations of the infinite planes are

a(x – 1) + b(y – 1) + c(z + 1) = 0, where 5a + 3b – 4c = 0.