Find the equation of the plane which contains the line of intersection of the plane x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and whose x – intercept is twice of z – intercept. Hence, write the equation of the plane passing through the point (2,3, – 1) and parallel to the plane obtained above?
We know that equation of plane passing through the line of intersection of planes
(a1x + b1y + c1z + d1) + k(a2x + b2y + c2z + d2) = 0
So equation of plane passing through the line of intersection of planes
x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 is
x + 2y + 3z – 4 + k(2x + y – z + 5) = 0
x(1 + 2k) + y(2 + k) + z(3 – k) – 4 + 5k = 0
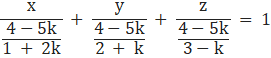
as given that x–intercept is twice of z intercept
so ![]()
3 – k = 2(1 + 2k)
3 – k = 2 + 4k
5k = 1
![]()
Put this value in equation (1)
x(1 + 2k) + y(2 + k) + z(3 – k) – 4 + 5k = 0
x(1 + ![]() ) + y(2 +
) + y(2 + ![]() ) + z(3 –
) + z(3 – ![]() ) – 4 +
) – 4 + ![]() = 0
= 0
x(![]() ) + y(
) + y(![]() ) + z(
) + z(![]() ) – 3 = 0
) – 3 = 0
multiply by 5
7x + 11y + 14z = 15 …… (2)
And equation of the plane passing through the point is
a1(x – x1) + b1(y – y1) + c1(z – z1) = 0
and point is (2,3, – 1) so that,
a1(x – 2) + b1(y – 3) + c1(z + 1) = 0
by equation (2) a1 = 7,b1 = 11,c1 = 14
so 7(x – 2) + 11(y – 3) + 14(z + 1) = 0
7x + 11y + 14z – 14 – 33 + 14 = 0
7x + 11y + 14z – 33 = 0