Find the shortest distance between the lines and

Let the two lines be l₁ and l₂.

So, and

We need to find the shortest distance between l₁ and l₂.

Recall the shortest distance between the lines: and is given by

Here, (x₁, y₁, z₁) = (–1, –1, –1) and (x₂, y₂, z₂) = (3, 5, 7)

Also (a₁, b₁, c₁) = (7, –6, 1) and (a₂, b₂, c₂) = (1, –2, 1)

We will evaluate the numerator first.

Let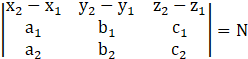

⇒ N = (4)[(–6)(1) – (–2)(1)] – (6)[(7)(1) – (1)(1)] + (8)[(7)(–2) – (1)(–6)]

⇒ N = 4(–6 + 2) – 6(7 – 1) + 8(–14 + 6)

⇒ N = –16 – 36 – 64

∴ N = –116

Now, we will evaluate the denominator.

Let

b₁c₂ – b₂c₁ = (–6)(1) – (–2)(1) = –6 + 2 = –4

c₁a₂ – c₂a₁ = (1)(1) – (1)(7) = 1 – 7 = –6

a₁b₂ – a₂b₁ = (7)(–2) – (1)(–6) = –14 + 6 = –8

So, shortest distance =

Thus, the required shortest distance is units.