Write each of the following in the simplest form:
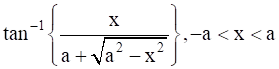
Assume x = a sinθ
= tan–1
= tan–1
= tan–1
= tan–1
= tan–1
Cos θ = cos2
– sin2
and sinθ = 
,cos2
+ sin2
= 1
= tan–1
= tan–1
= tan–1
= tan–1(tan
)
= 
But θ = sin–1
∴ The given equation simplification to sin–1
.
7