D, E and F are respectively the mid-points of sides AB, BC and CA of Δ ABC. Find the ratio of the areas of ΔDEF and Δ ABC

Question

D, E and F are respectively the mid-points of sides AB, BC and CA of &Delta; ABC. Find the ratio of the areas of &Delta;DEF and &Delta; ABC

Philoid · Accepted Answer

Given:

Because D, E and F are respectively the mid-points of sides AB, BC and CA of Δ ABC,

Therefore, From mid-point theorem,

DE || AC and DE = AC

DF || BC and DF = BC

EF || AC and EF = AB

Now, In ΔBED and ΔBCD

∠BED =∠ BCA (Corresponding angles)

∠BDE = ∠BAC (Corresponding angles)

∠EBD = ∠CBA (Common angles)

Therefore,

ΔBED ~ ΔBCA (From the AAA similarity)

=

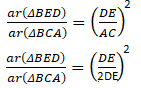
ar(ΔBED) = ar(ΔBCA)

Similarly,

ar(ΔCFE) = ar(ΔCBA)

And,

ar(ΔADF) = ar(ΔABC)

Also,

ar(ΔDEF) = ar(ΔABC) – [ar(ΔBED) + ar(ΔCFE) + ar(ΔADF)]

ar(ΔDEF) = ar(ΔABC) –

= ar(ΔABC)

=