A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 
find the length of the wire
The figure is given below:
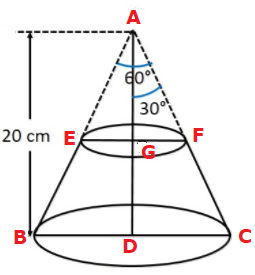
In ΔAEG,
⇒ EG = tan 300 × AG
⇒ EG = (1/√3)× 10 cm
⇒ EG = 
In ΔABD,
= tan 30o
⇒ BD = tan 300 × AD
⇒ BD =(1/√3)× 20 cm
⇒ BD = 
⇒ BD = 
Radius (r1) = 
cm
Radius (r2) = 
cm
Height (h) = 10 cm
Volume of frustum = (1/3)πh (r12 + r22 + r1r2)
= 
* π * 10 [(
)2 + (
)2 + 
]
= 
[
+ 
+ 
]
= 
* 
* 
= 
cm3
Radius (r) of wire =
* 
= 
cm
Let the length of wire be l.
Volume of wire = Area of cross-section × Length
= (πr2) (l)
= π * (
)2 * l
Volume of frustum = Volume of wire
= 
* (
)2 * l
* 1024 = l
l = 796444.44 cm
= 7964.44 meters