Prove that the lengths of tangents drawn from an external point to a circle are equal.
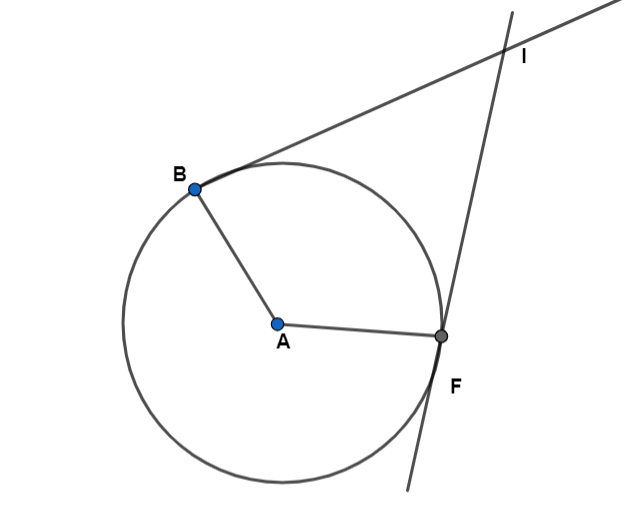
Given:
• Circle with centre A
• Tangents IB and IF
Proof:
In ∆ ABI and ∆ AFI
• AB = AF = Radius of the circle
• ∠ ABI = ∠ AFI = 90°
(∵ tangents are perpendicular to the radius)
• AI = AI (common side)
So, by RHS rule, ∆ ABI ≅ ∆AFI
⇒ BI = FI
(∵ corresponding sides of congruent triangles are equal)
Hence, the lengths of tangents drawn from an external point to a circle are equal.
18