Prove that the lengths of the tangents drawn from an external point to a circle are equal. Using the above theorem, prove that AB+CD = AD+BC, if a quadrilateral ABCD is drawn to circumscribe a circle.

Question

Philoid · Accepted Answer

Proof of theorem

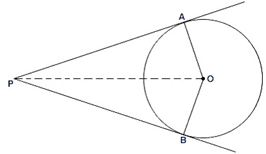
Let us consider a circle with center O, AP and BP be two common tangents to it from an external point P.

Join OP.

To Prove: AP = BP

Proof:

In ΔAOP and ΔBOP

OA = OB [Radii of same circle]

OP = OP [Common]

∠OAP = ∠OBP [Both 90° as tangent at a point on the circle is perpendicular to the radius through point of contact]

⇒ ΔAOP ≅ ΔBOP [By RHS congruency criterion]

⇒ AP = BP [Corresponding parts of congruent triangles are equal]

Hence, the lengths of the tangents drawn from an external point to a circle are equal.

Proof of AB + CD = AD + BC

Given: A quadrilateral ABCD is drawn to circumscribe a circle with center O. Circle touches sides AB, BC, CD and AD at points P, Q, R and S respectively.

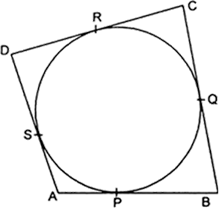
To prove: AB + CD = AD + BC

Proof:

We know, tangents drawn from an external point to a circle are equal.

In the figure, we observe

AP = AS [Tangents from point A]

BP = BQ [Tangents from point B]

CR = CQ [Tangents from point C]

DR = DS [Tangents from point D]

Adding the above four equations, we get

AP + BP + CR + DR = AS + BQ + CQ + DS

⇒ AB + CD = AS + DS + BQ + CQ

⇒ AB + CD = AD + BC

Hence Proved!