Four equal circles are described at the four corners of a square so that each touches two of the others. The shaded area enclosed between the circles is cm², Find the radius of each circle.

Question

Four equal circles are described at the four corners of a square so that each touches two of the others. The shaded area enclosed between the circles is cm 2 , Find the radius of each circle.

Philoid · Accepted Answer

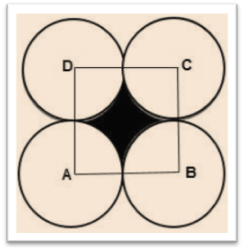
Let the side of square be ‘a’ and radius of circle be ‘r’

We observe from the figure,

Side of square = 2 × radius of circle

⇒ a = 2r

Also, we know

Area of square = (side)²

Area of quadrant , where r denotes radius

Area of enclosed region = area of square – area of 4 quadrants

⇒ 24 = 6r²

⇒ r² = 4

⇒ r = 2 cm

Hence, radius of circle is 2 cm

Four equal circles are described at the four corners of a square so that each touches two of the others. The shaded area enclosed between the circles is cm2, Find the radius of each circle.

Four equal circles are described at the four corners of a square so that each touches two of the others. The shaded area enclosed between the circles is cm², Find the radius of each circle.