If 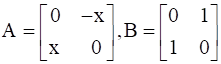and x 2 = – 1, then show that (A + B) 2 = A 2 + B 2 .

Question

Philoid · Accepted Answer

Given, and x² = –1.

We need to prove (A + B)² = A² + B².

Let us evaluate the LHS and the RHS one at a time.

To find the LHS, we will first calculate A + B.

We know (A + B)² = (A + B)(A + B).

(∵ x² = –1)

To find the RHS, we will first calculate A² and B².

We know A² = A × A.

(∵ x² = –1)

Similarly, we also have B² = B × B.

Now, the RHS is A² + B².

Thus, (A + B)² = A² + B².

If and x2 = – 1, then show that (A + B)2 = A2 + B2.