If then prove by principle of mathematical induction that for all n ∈ N.

Given.

We need to prove that using the principle of mathematical induction.

Step 1: When n = 1, we have

Hence, the equation is true for n = 1.

Step 2: Let us assume the equation true for some n = k, where k is a positive integer.

To prove the given equation using mathematical induction, we have to show that.

We know A^k+1 = A^k × A.

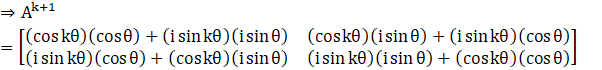
However, we have i² = –1

Hence, the equation is true for n = k + 1 under the assumption that it is true for n = k.

Therefore, by the principle of mathematical induction, the equation is true for all positive integer values of n.

Thus, for all n ϵ N.