If prove that for all

Given.

We need to prove that.

We will prove this result using the principle of mathematical induction.

Step 1: When n = 1, we have

Hence, the equation is true for n = 1.

Step 2: Let us assume the equation true for some n = k, where k is a positive integer.

To prove the given equation using mathematical induction, we have to show that.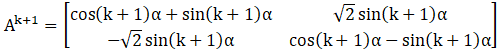

We know A^k+1 = A^k × A.

We evaluate each value of this matrix independently.

(a) The value at index (1, 1)

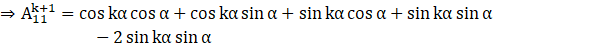
(b) The value at index (1, 2)

(c) The value at index (2, 1)

(d) The value at index (2, 2)

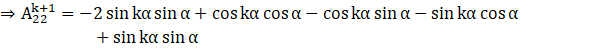
So, the matrix A^k+1 is

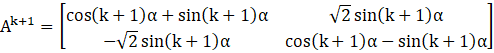
Hence, the equation is true for n = k + 1 under the assumption that it is true for n = k.

Therefore, by the principle of mathematical induction, the equation is true for all positive integer values of n.

Thus, for all n ϵ N.