Write the minors and cofactors of each element of the first column of the following matrices and hence evaluate the determinant in each case:

Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column.

The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

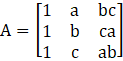
M₁₁ = b × ab – c × ca

M₁₁ = ab² – ac²

M₂₁ = a × ab – c × bc

M₂₁ = a²b – c²b

M₃₁ = a × ca – b × bc

M₃₁ = a²c – b²c

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × (ab² – ac²)

= ab² – ac²

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × (a²b – c²b)

= c²b – a²b

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × (a²c – b²c)

= a²c – b²c

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁

= 1× (ab² – ac²) + 1 × (c²b – a²b) + 1× (a²c – b²c)

= ab² – ac² + c²b – a²b + a²c – b²c