For what value of x matrix A is singular?

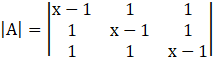
Expanding along the first row

= (x–1) ((x–1) (x–1)– 1×1) – 1((x–1) – 1×1) + 1(1×1 – 1×(x–1))

= (x–1) (x² – 2x + 1 – 1) – 1(x–1 – 1) + 1(1 – x+1)

= x(x–1) (x– 2) – 1(x–2) – (x–2)

= (x– 2) {x(x–1) – 1 – 1}

= (x– 2) (x² – x – 2)

For singular |A| = 0,

(x– 2) (x² – x – 2) = 0

(x– 2) (x² – 2x + x – 2) = 0

(x–2)(x–2)(x+1) = 0

∴ x = –1 or 2

Also |A| = 28

⇒ 7x² + 3x – 6 =28

⇒ 7x² + 3x – 34 = 0

⇒ 7x² + 17x – 14x – 34 = 0

⇒ x(7x+ 17) – 2(7x +17) = 0

⇒ (x–2)(7x +17) = 0