Without expanding, show that the value of each of the following determinants is zero:

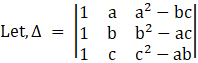
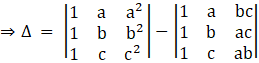
Applying R₂→R₂ – R₁ and R₃ → R₃ – R₁, we get,

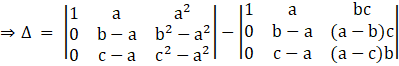
Taking (b – a) and (c – a) common from R₂ and R₃ respectively,

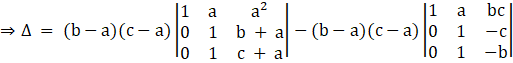
= [(b – a)(c – a)][(c + a) – (b + a) – ( – b + c)]

= [(b – a)(c – a)][c + a + b – a – b – c]

= [(b – a)(c – a)][0] = 0