Without expanding, show that the value of each of the following determinants is zero:

, where A, B, C are the angles of ΔABC.

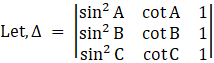
Now,

Δ = sin² A (cot B – cot C) – cot A (sin² B – sin² C) + 1 (sin²B cot C – cot B sin² C

As A, B and C are angles of a triangle,

A + B + C = 180°

Δ = sin² A cot B – sin² A cot C – cot A sin² B + cot A sin²C + sin²B cot C – cot B sin² C

By using formulae,

Δ = 0

Hence, Proved.