Prove the following identities:

Question

Philoid · Accepted Answer

L.H.S =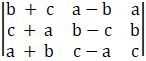

As |A| = |A|^T

So,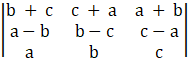

If any two rows or columns of the determinant are interchanged, then determinant changes its sign

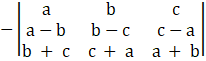
Apply C₁→C₁ + C₂ + C₃

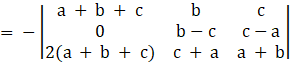
Taking (a + b + c) common from C₁ we get,

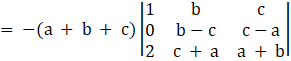
Applying, R₃→R₃ – 2R₁

= – (a + b + c)[(b – c)(a + b – 2c) – (c – a)(c + a – 2b)]

= 3abc – a³ – b³ – c³

As, L.H.S = R.H.S, hence proved.