Prove the following identities:

![]()
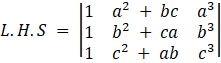
Applying, R2→R2 – R1, and R3→R3 – R1
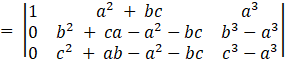
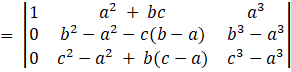
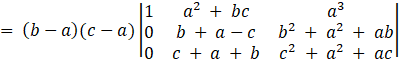
= (b – a)(c – a)[((b + a – c))(c2 + a2 + ac) – (b2 + a2 + ab)(c2 + a2 + ac)]
= – (a – b)(c – a)(b – c)(a2 + b2 + c2)
= R.H.S
Hence, proved.
23
Prove the following identities:

![]()
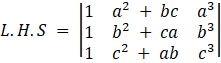
Applying, R2→R2 – R1, and R3→R3 – R1
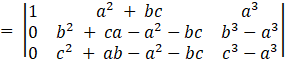
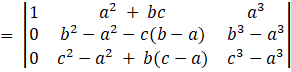
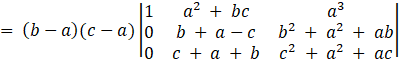
= (b – a)(c – a)[((b + a – c))(c2 + a2 + ac) – (b2 + a2 + ab)(c2 + a2 + ac)]
= – (a – b)(c – a)(b – c)(a2 + b2 + c2)
= R.H.S
Hence, proved.