Prove the following identities –

Question

Philoid · Accepted Answer

Let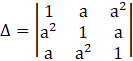

Recall that the value of a determinant remains same if we apply the operation R_i→ R_i + kR_j or C_i→ C_i + kC_j.

Applying R₁→ R₁ + R₂, we get

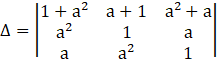
Applying R₁→ R₁ + R₃, we get

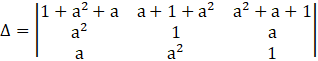
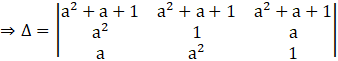
Taking the term (a² + a + 1) common from R₁, we get

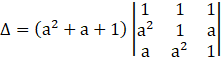
Applying C₂→ C₂ – C₁, we get

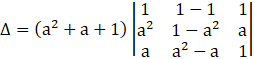
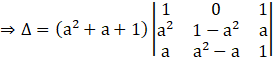
Applying C₃→ C₃ – C₁, we get

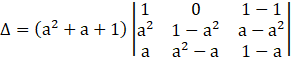
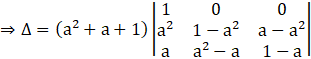
Expanding the determinant along R₁, we have

Δ = (a² + a + 1)(1)[(1 – a²)(1 – a) – (a² – a)(a – a²)]

⇒ Δ = (a² + a + 1)(1 – a – a² + a³ – a³ + a⁴ + a² – a³)

⇒ Δ = (a² + a + 1)(1 – a – a³ + a⁴)

⇒ Δ = (a² + a + 1)(a⁴ – a³ – a + 1)

⇒ Δ = (a² + a + 1)[a³(a – 1) – (a – 1)]

⇒ Δ = (a² + a + 1)(a – 1)(a³ – 1)

⇒ Δ = (a – 1)(a² + a + 1)(a³ – 1)

⇒ Δ = (a³ – 1)(a³ – 1)

∴ Δ = (a³ – 1)²

Thus,