Prove the following identities –

Let 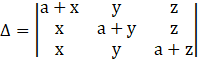
Recall that the value of a determinant remains same if we apply the operation Ri→ Ri + kRj or Ci→ Ci + kCj.
Applying C1→ C1 + C2, we get
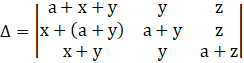
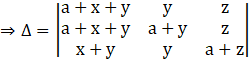
Applying C1→ C1 + C3, we get
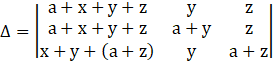
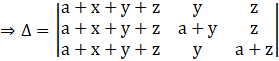
Taking the term (a + x + y + z) common from C1, we get
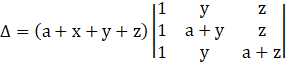
Applying R2→ R2 – R1, we get
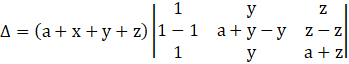
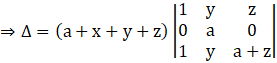
Applying R3→ R3 – R1, we get
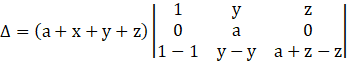
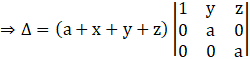
Expanding the determinant along C1, we have
Δ = (a + x + y + z)(1)[(a)(a) – (0)(0)]
⇒ Δ = (a + x + y + z)(a)(a)
∴ Δ = a2(a + x + y + z)
Thus, 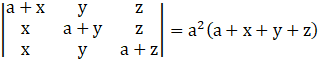
44