Find the value of x if the area of a triangle is 35 square cms with vertices (x, 4), (2, – 6) and (5, 4).

Given: – Vertices of triangle are (x, 4), (2, – 6) and (5, 4) and area of triangle is 35 sq.cms

Tip: – If vertices of a triangle are (x₁,y₁), (x₂,y₂) and (x₃,y₃), then the area of the triangle is given by:

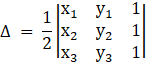
Now,

Substituting given value in above formula

⇒

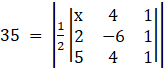
Removing modulus

⇒

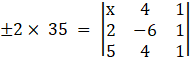
Expanding along R₁

⇒

⇒ [x(– 10) – 4(– 3) + 1(8 – 30)] = ± 70

⇒ [ – 10x + 12 + 38] = ± 70

⇒ ±70 = – 10x + 50

Taking + ve sign, we get

⇒ + 70 = – 10x + 50

⇒ 10x = – 20

⇒ x = – 2

Taking – ve sign, we get

⇒ – 70 = – 10x + 50

⇒ 10x = 120

⇒ x = 12

Thus x = – 2, 12