If the points (3, – 2), (x,2) and (8,8) are collinear, find x using determinant.
Given: – (3, – 2), (x,2) and (8,8) are collinear points
Tip: – For Three points to be collinear, the area of the triangle formed by these points will be zero
Now, we know that,
Vertices of a triangle are (x1,y1), (x2,y2) and (x3,y3), then the area of the triangle is given by:
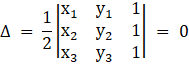
Now,
Substituting given value in above formula
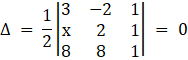
⇒ 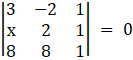
Expanding along R1
⇒ ![]()
⇒ [x(– 6) + 2(x – 8) + 1(8x – 16)] = 0
⇒ – 6x + 2x – 16 + 8x – 16 = 0
⇒ 10x = 50
⇒ x = 5
11