Solve each of the following systems of homogeneous linear equations:

2x + 3y + 4z = 0

X + y + z = 0

2x + 5y – 2z = 0

Given Equations:

2x + 3y + 4z = 0

X + y + z = 0

2x + 5y – 2z = 0

Any system of equation can be written in matrix form as AX = B

Now finding the Determinant of these set of equations,

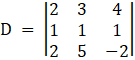
= 2(1×(– 2) – 1×5) – 3(1×(– 2) – 2×1) + 4(1×5 – 2×1)

= 2(– 2 – 5) – 3(– 2 – 2) + 4(5 – 2)

= 1×(– 7) – 3 × (– 4) + 4×3

= – 7 + 12 + 12

= 17

Since D ≠ 0, so the system of equation has infinite solution.

Therefore the system of equation has only solution as x = y = z = 0.