If a,b,c are non – zero real numbers and if the system of equations

(a – 1) x = y + z

(b – 1) y = z + x

(c – 1) z = x + y

Has a non – trivial solution, then prove that ab + bc + ca = abc.

Given Equations:

(a – 1) x = y + z

(b – 1) y = z + x

(c – 1) z = x + y

Rearranging these equations

(a – 1)x – y – z = 0

– x + (b – 1)y – z = 0

– x – y + (c – 1)z = 0

For trivial solution D = 0

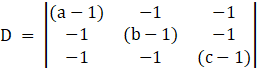
= (a – 1)((b – 1)(c – 1) – (– 1)×(– 1)) + 1(– 1(c – 1) – (– 1)×(– 1)) – 1((– 1)×(– 1) + (b – 1))

= (a – 1)(bc –b –c + 1 – 1) + (1 – c – 1) – 1(1 + b – 1))

= (a – 1)(bc –b –c) –c –b

= abc –ab –ac –bc + b + c – b – c

= abc –ab –ac –bc

Now D = 0

⇒ abc – ab – ac – bc = 0

⇒ abc = ab + bc + ac

Hence proved.