A function f(x) is defined as 
Show that f(x) is continuous at x = 3.
Ideas required to solve the problem:
1. Meaning of continuity of function – If we talk about a general meaning of continuity of a function f(x), we can say that if we plot the coordinates (x, f(x)) and try to join all those points in the specified region, we can do so without picking our pen i.e you will put your pen/pencil on graph paper and you can draw the curve without any breakage.
Mathematically we define the same thing as given below:
A function f(x) is said to be continuous at x = c where c is x–coordinate of the point at which continuity is to be checked
If:–
![]() equation 1
equation 1
where h is a very small positive no (can assume h = 0.00000000001 like this )
It means:–
Limiting the value of the left neighborhood of x = c also called left–hand limit LHL ![]() must be equal to limiting value of right neighborhood of x= c called right hand limit RHL
must be equal to limiting value of right neighborhood of x= c called right hand limit RHL ![]() and both must be equal to the value of f(x) at x=c i.e. f(c).
and both must be equal to the value of f(x) at x=c i.e. f(c).
Thus, it is the necessary condition for a function to be continuous
So, whenever we check continuity we try to check above equality if it holds, function is continuous else it is discontinuous.
Let’s solve :
To prove function is continuous at x=3, we need to show LHL = RHL = f(c) As continuity is to be checked at x = 3 therefore c=3 (in equation 1)
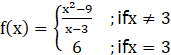 …… eqn 2
…… eqn 2
From eqn 2 :
f(3) = 6
LHL = ![]()
Using equation 2 –
![]()
![]()
RHL = ![]()
![]()
![]()
Clearly, LHL = RHL = f(3) = 6
∴ f(x) is continuous at x=3