For what value of is the function 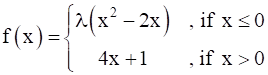continuous at x = 0? What about continuity at x = ± 1?

we have to find the value of '' such that f(x) is continuous at x = 0

If f(x) is be continuous at x = 0,then, f(0)^–=f(0) ⁺ =f(0)

LHL = f(0)^–=

⇒ (0² + 2×0)

⇒ 0 ...(1)

RHL = f(0) ⁺ =

⇒ 4(0) + 1

⇒ 1 ...(2)

From (1) & (2),we get f(0)^–=f(0) ⁺ ,

Hence f(x) is not continuous at x = 0

we also have to find out the continuity at point

For f(x) is be continuous at x = 1,

then ,f(0)^–=f(0) ⁺ =f(0)

LHL = f(1) ⁺ =

⇒ (0²–1)

⇒ – ...(1)

RHL = f(1) ^{+ =}

⇒ (5 + 4×0)

⇒ 5 ...(2)

From (1) & (2),we get f(0)^– ₌ f(0) ⁺ ,

i.e, – = 5

⇒ = –5

Hence f(x) is continuous at x = 1,when = –5

Similarly, For f(x) is be continuous at x = –1,

then ,f(–1)^–=f(–1) ⁺ =f(–1)

LHL = f(–1)^–=

⇒ –(0² + 4×0 + 3)

⇒ –3 ...(3)

RHL = f(–1) ⁺ =

⇒ (–3 + 4×0)

⇒ –3 ...(2)

From (1) & (2),we get, f(–1)^–=f(–1) ⁺

i.e, –3 = –3

⇒ = 1

Hence f(x) is continuous at x = 1,when = 1