Find the points of discontinuity, if any, of the following functions :

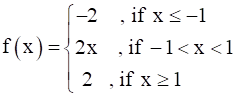
Basic Idea:

A real function f is said to be continuous at x = c, where c is any point in the domain of f if :

where h is a very small ‘+ve’ no.

i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.

This is very precise, using our fundamental idea of limit from class 11 we can summarise it as, A function is continuous at x = c if :

Here we have,

……….equation 1

Function is defined for all real numbers so we need to comment about its continuity for all numbers in its domain (domain = set of numbers for which f is defined)

For x < –1, f(x) is having a constant value, so the curve is going to be straight line parallel to x–axis.

So, it is everywhere continuous for x < –1.

It can be verified using limits as discussed in previous problems

Similarly for –1 < x < 1, plot on X–Y plane is a straight line passing through origin.

So, it is everywhere continuous for –1 < x < 1.

And similarly for x > 1, plot is going to be again a straight line parallel to x–axis

∴ it is also everywhere continuous for x > 1

From graph it is clear that function is continuous everywhere but let’s verify it with limits also.

As x = –1 is a point at which function is changing its nature so we need to check the continuity here.

f(–1) = –2 [using eqn 1]

LHL =

RHL =

Thus LHL = RHL = f(–1)

∴ f(x) is continuous at x = –1

Also at x = 1 function is changing its nature so we need to check the continuity here too.

f(1) = 2 [using eqn 1]

LHL =

RHL =

Thus LHL = RHL = f(1)

∴ f(x) is continuous at x = 1

Thus, f(x) is continuous everywhere and there is no point of discontinuity.